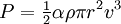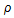
where
P = power in watts,
a = factor determined by the design of the turbine,
= mass density of air in kilograms per cubic meter,
r = radius of the wind turbine in meters, and v = velocity of the air in meters per second.
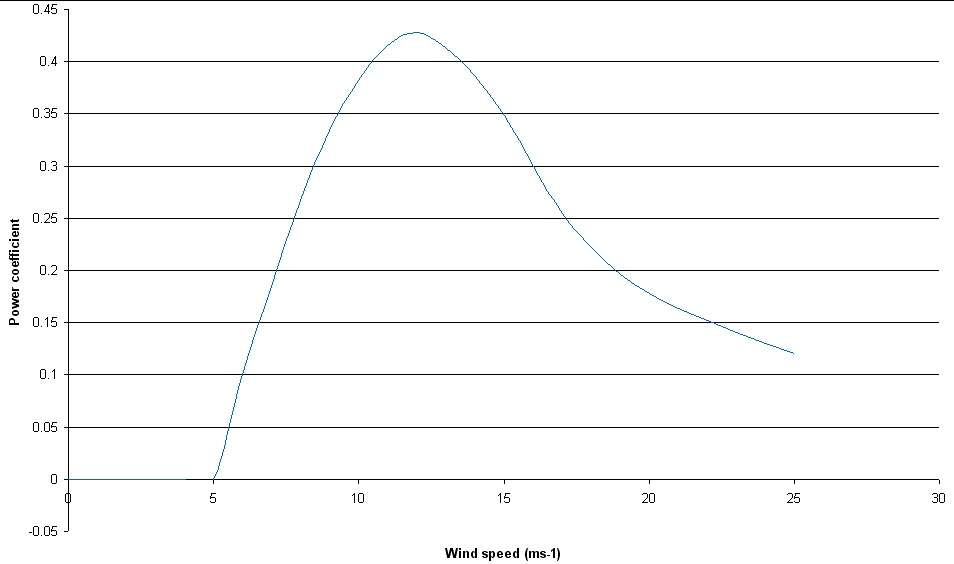
As the wind turbine extracts energy from the air flow, the air is slowed down, which causes it to spread out. Albert Betz , a German physicist, determined in 1919 (see Betz' law ) that a wind turbine can extract at most 59% of the energy that would otherwise flow through the turbine's cross section, that is a can never be higher than 0.59 in the above equation. The Betz limit applies regardless of the design of the turbine.
This equation shows the effects of the mass rate of flow of air traveling through the turbine, and the energy of each unit mass of air flow caused by its velocity. As an example, on a cool 15 °C (59 °F) day at sea level, air density is 1.225 kilograms per cubic metre. An 8 m/s (28.8 km/h or 18 mi/h) breeze blowing through a 100 meter diameter rotor would move almost 77,000 kilograms of air per second through the swept area. The total power of the example breeze through a 100 meter diameter rotor would be about 2.5 megawatts. Betz' law states that no more than 1.5 megawatts could be extracted.
P = power in watts,
a = factor determined by the design of the turbine,
= mass density of air in kilograms per cubic meter,
r = radius of the wind turbine in meters, and v = velocity of the air in meters per second.
As the wind turbine extracts energy from the air flow, the air is slowed down, which causes it to spread out. Albert Betz , a German physicist, determined in 1919 (see Betz' law ) that a wind turbine can extract at most 59% of the energy that would otherwise flow through the turbine's cross section, that is a can never be higher than 0.59 in the above equation. The Betz limit applies regardless of the design of the turbine.
This equation shows the effects of the mass rate of flow of air traveling through the turbine, and the energy of each unit mass of air flow caused by its velocity. As an example, on a cool 15 °C (59 °F) day at sea level, air density is 1.225 kilograms per cubic metre. An 8 m/s (28.8 km/h or 18 mi/h) breeze blowing through a 100 meter diameter rotor would move almost 77,000 kilograms of air per second through the swept area. The total power of the example breeze through a 100 meter diameter rotor would be about 2.5 megawatts. Betz' law states that no more than 1.5 megawatts could be extracted.
The amount of power transferred to a wind turbine is directly proportional to the area swept out by the rotor, to the density of the air, and the cube of the wind speed.
The power P in the wind is given by:
The power P in the wind is given by:
Wind Generator Features