Time-dependent numerical prediction of the fuel premixing process within an aero-propulsion combustion system
Prof. Ferruccio Pittaluga - DIMSET - Univ. of Genova
Scope of the Presentation
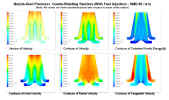
The investigation here presented is centred on the two-phase flow-process that takes place in the premixer section of the new Fiat-Avio aero-engine burner, with a two-swirler, inward-flow configuration and liquid fuel injection from a single, conical-spray injector located on the centreline.
The primary objective of significantly reducing the pollutant emissions, particularly in terms of NOx and CO, has addressed the overall design strategy toward a so-called LPP (lean premixing prevaporising) solution, which, by itself, specifies the expected performance but does not help configuring any specific geometry.
The burner-optimisation strategy here pursued is based on the performance trend-capturing concept, wherein a “targeted” sequential application is performed, of a time-dependent 3D Navier-Stokes solver, in order to reach the expected design and operational objectives.
These latter are essentially those of:
• an adequate level to be attained for the vaporisation and premixing process
• a safe stability-margin of the overall flow process
• and a proper swirl level of the flow at premixer outlet
The Navier Stokes Solver NastComb
The burner-design strategy was pursued by means of an extensive, sequential application of NastComb, a 3D, “ALE” (Arbitrary Lagrangian Eulerian) time-dependent Navier-Stokes solver for turbulent multi-phase reactive flows which, since more than twelve years, is undergoing a continuous development at DIMSET mainly for gas turbine combustor analysis, both in unreactive and reactive situations (see Refs. already given).
The turbulence scheme is quite peculiar: it solves a 3-equation time-dependent TSDIA-consistent model (Two-Scale Direct Interaction Approximation), extended to treat compressible, variable-density turbulence by means of an MTS procedure (Markovianised Two-Scale). A recent ensemble-average reformulation of the code’s previous favre-averaged scheme has allowed NastComb to acquire VLES (Very Large Eddy Simulation) capability.
The ensemble-averaged (unreactive) governing eqs., together with the three-eq. turbulence model, are as follows:
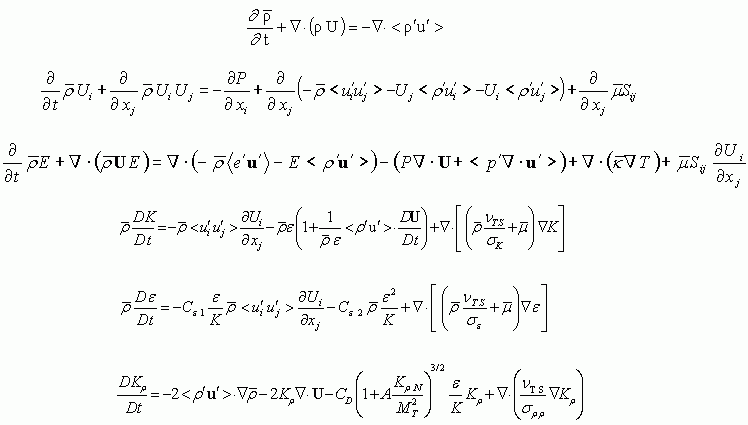
Liquid-Fuel Spray Modelisation in NastComb: Latest Developments
With reference to liquid-fuel spray modelisation, NastComb implements a rather advanced scheme, wherein a solution is pursued in terms of a droplet probability distribution function f involving 10 independent variables in addition to time, namely the position vector, the velocity vector, the droplet radius, the droplet temperature, the distortion from sphericity y (governing secondary break-up, typically for y>1.0) and its time rate of change. The time evolution of the droplet pdf (i.e. the function f ) is obtained by solving a form of the spray equation inclusive of the droplet source terms, produced by collisional and aerodynamic break-up processes.
In order to take care, in a more specific fashion, of the peculiar characteristics of the gas-turbine burners, the spray model already implemented in NastComb code, has been extended and optimized, along the following lines.
Nastcomb was originally provided with the so called TAB model (or Taylor Analogy Break-up model). The analogy between a deforming drop and a spring-mass system leads to a differential equation for the description of the temporal evolution of the deformation occurring on the surface of a liquid droplet:
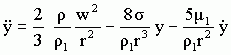

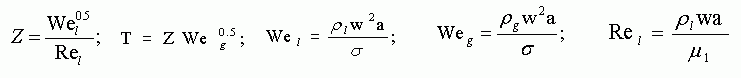
The break up time of a blob, that is the time before the instability has reached a relevant dimension, is then given by:
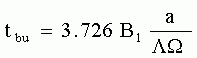
Once a blob has broken up, new droplets have to be created with a radius that is related with the faster wavelength:
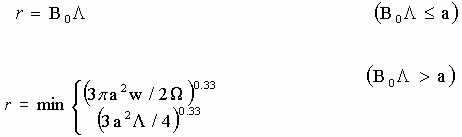
B0 is a constant parameter of order unity which has to be determined through experimental results (such as B1 in the previous formulation).
While the blobs primary break up is mainly influenced by the Kelvin-Helmholtz waves grow-up process, the secondary break up of the droplets, formed from the blobs, can be modeled considering also other types of instabilities, such as the so called Rayleigh-Taylor instability, connected with the acceleration experimented by the liquid. In the same way as before, expression for the faster growing wave characteristic and for the relative breakup time are derived from a mathematical model.
The introduction of this new breakup model in NastComb code has enhanced its flexibility: indeed, different complementary breakup models, that can be used separately or partially overlapped, can better capture the many different physical aspects involved in the problems of jet and spray breakup.
Pictures
Research Projects